Look at this sequence: 1/4, 1/16, 1/64, 1/256, …
What do you think is the value when adding up the terms of this sequence? The surprising answer is 1/3. If you find this answer surprising indeed, read on to figure out how this came to be.
So our sum is 1/4 + 1/16 + 1/64 + 1/256 + … = 1/3
The sequence we deal with here is a geometric sequence. In a geometric sequence each term is found by multiplying the previous term by a constant.
In General you could write a Geometric Sequence like this:
{a, ar, ar2, ar3, … }
Note, each term of our sequence can be computed with this rule: xn = ar(n-1). Also note this sequence goes to infinity, ….
There exists a formula to compute the value of infinite sequences:
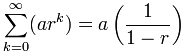
Filling in the values, a=1 and r=1/4, the sum of our infinite sequence is = 1/(1-1/4) = 4/3
Because we have dropped the first value of this sequence (1/4)0 = 1 we have to subtract it from the result to reach the final answer 4/3 – 1 = 1/3.
The picture visualizes our sequence (1/4, 1/16, … ) as the green area in a square. Do you also feel the sum of the green area makes about 1/3 of the square’s entire area?
For more help with sequences get a personal math tutor.



5 Responses to Sum of Infinite Geometric Sequence Equals 1/3